Cours de chimie Organique -
Eléments de spectroscopie de RMN
Introduction
La découverte fondatrice de la résonance magnétique nucléaire est le fait du physicien américain d'origine austro-hongroise, I. Rabi. Ce dernier a obtenu le prix Nobel de physique en 1944 pour ses études concernant le moment magnétique du noyau [51].
Le phénomène physique sur lequel repose la résonance magnétique nucléaire (RMN) a été étudié en 1946 par des groupes de physiciens dirigés par E. M. Purcell (Université de Harvard) et F. Bloch (Université de Stanford) [25] ; [41]. Depuis cette date, la technique a connu un développement spectaculaire dans différents domaines. La RMN apporte des renseignements extrêmement intéressants sur la structure des molécules aussi bien en phase liquide qu'en phase solide.
Richard Ernst a obtenu le prix Nobel de chimie en 1991 pour la mise au point de la spectroscopie de RMN impulsionnelle [26].
Dans le domaine de la biochimie, le prix Nobel 2002 a été attribué à K. Wüthrich pour ses travaux concernant la structure tridimensionnelle des macromolécules [27].
L'imagerie par résonance magnétique (IRM) constitue une méthode très utile pour visualiser les tissus mous des organismes vivants. Cette découverte d'intérêt majeur a été récompensée par l'attribution du prix Nobel de physiologie et médecine à P.C. Lauterbur et P. Mansfield en 2003 [44].
Une passionante histoire de la RMN par Maurice Goldman qui en fut l'un des acteurs se trouve à la référence [28]. Théorie classique pour un noyau unique dans un champ magnétique en l'absence d'environnement chimique
Moment magnétique
En théorie classique, le moment cinétique intrinsèque d'un noyau est lié à sa rotation propre (à ne pas confondre avec le moment cinétique rotationnel). Du point de vue magnétique, un noyau de moment cinétique intrinsèque non nul I, possède un moment magnétique nucléaire qui est représentable par un vecteur m colinéaire à I. On traduit cela par la relation :
g est appelée constante gyromagnétique. Pour le proton cette constante vaut :
|
Noyau
|
19F
|
13C
|
31P
|
1H
|
|
g (rad.T-1.s-1)
|
2,518.108
|
0,6728.108
|
1,084.108
|
2,67.108
|
Précession de Larmor
Dans tout ce qui suit le référentiel du laboratoire, supposé galiléen, sera noté R0. Le moment magnétique d'un noyau de moment cinétique intrinsèque I a pour expression :
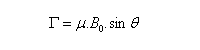
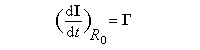
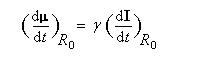
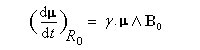
- premièrement, nous voyons que :
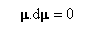 Ce qui signifie que le moment magnétique m possède un module constant.
Ce qui signifie que le moment magnétique m possède un module constant.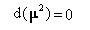
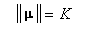
- deuxièmement :
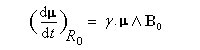
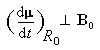 L'angle entre le moment magnétique m et le champ magnétique B0 est donc constant.
L'angle entre le moment magnétique m et le champ magnétique B0 est donc constant.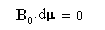
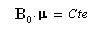
- Enfin nous voyons que nous pouvons mettre l'équation sous la forme :
Le mouvement de l'extrémité du vecteur moment magnétique m est un cercle. Le vecteur moment magnétique effectue un mouvement de précession autour de la direction du champ magnétique. L'application d'un champ magnétique statique externe B0,. Ce mouvement s'appelle précession de Larmor. Le vecteur vitesse angulaire a pour expression :
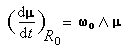
La vitesse angulaire w0 de précession du vecteur m autour de la direction du champ B0 vaut :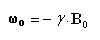
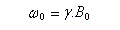 On notera que cette vitesse angulaire de précession est proportionnelle au champ appliqué.
On notera que cette vitesse angulaire de précession est proportionnelle au champ appliqué.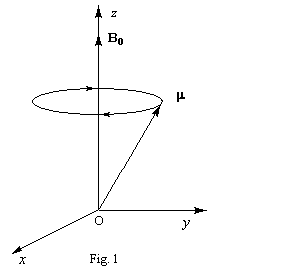
|
Noyau
|
19F
|
13C
|
31P
|
|
n0 / MHz
|
40,06
|
17,24
|
9,71
|
L'énergie d'interaction entre le moment magnétique et le champ magnétique B0, s'écrit :
Nous avons vu plus haut que l'angle entre le moment magnétique m et le champ magnétique B0 est constant au cours du temps.
L'énergie est donc aussi constante au cours du temps :
Pour y parvenir, on va faire appel à un champ magnétique supplémentaire.
Absorption d'énergie, résonance
A ce stade, il est commode, pour simplifier l'étude cinématique, d'introduire un nouveau repère appelé repère tournant R (OXYZ). Il s'agit d'un repère dont l'axe OZ est confondu avec l'axe Oz du repère fixe du laboratoire R0 et dont les axes OX et OY tournent par rapport aux axes Ox et Oy respectivement, avec la vitesse angulaire de Larmor.
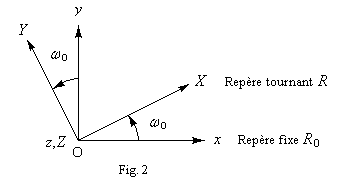
En suivant le même raisonnement que plus haut, on voit que le couple exercé par B1 va entraîner un nouveau mouvement de précession du moment magnétique, mais cette fois autour de l'axe OY (Fig. 3.)
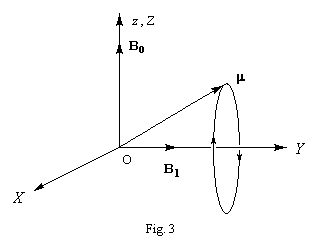
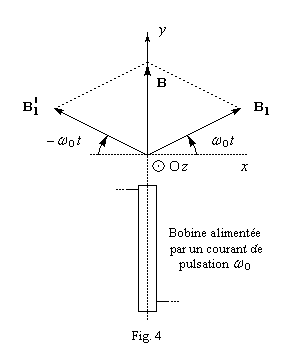 |
Un champ magnétique oscillant au cours du temps suivant une direction fixe (par exemple Oy) avec une pulsation w0 égale à la pulsation de Larmor. peut être considéré comme la somme de deux vecteurs tournant en sens inverse autour de la direction Oz, avec une vitesse angulaire w0. A un instant donné, les trois vecteurs champ sont en effet conformes au schéma ci-contre. Ce champ oscillant génère donc deux champs magnétiques B1 et B1' tournant en sens inverse à la vitesse angulaire w0. Seul le champ B1, qui garde une direction fixe, au cours du temps, dans le repère tournant (OXYZ) a une action sur le moment magnétique m . |
Spin nucléaire
Nous allons rechercher une description plus fidèle à la réalité physique en faisant intervenir un certain nombre de propriétés quantiques. Les conditions de quantification vont être introduites comme une "couche théorique" plaquée sur les équations classiques. Il s'agit donc d'un traitement qu'on qualifie de "semi-classique". Une approche satisfaisante de la RMN ne peut être faite qu'en utilisant la mécanique quantique (pour une introduction, voir par exemple : [48].)
Le spin nucléaire est une grandeur physique caractéristique d'un noyau qui permet de décrire ses propriétés magnétiques. Il s'agit d'une propriété quantique qui ne possède pas d'équivalent classique bien qu'une image élémentaire a consisté historiquement à l'associer à la rotation de la particule sur elle-même (to spin : tourner.) Le spin nucléaire peut être décrit par un opérateur vectoriel I de module ||I|| et dont la projection sur un axe fixe est notée Iz. Le choix de la direction verticale Oz comme axe de quantification est commode mais n'est pas impératif. Il est dicté par le fait que l'on choisit cet axe comme direction du champ magnétique statique dans la suite.
- le module ||I|| est quantifié. Il s'exprime en fonction du nombre quantique de spin nucléaire I, par la relation suivante
(h est la constante de Planck h = 6,62.10-34 J.s.) :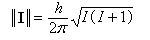
- la projection sur l'axe Oz, notée Iz, est également quantifiée :
Iz fait intervenir un second nombre quantique mI, prenant les valeurs :
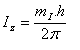
|
A
|
Z
|
I
|
Exemples
|
|
pair
|
pair
|
0
|
12C,16O,32S
|
|
pair
|
impair
|
entier
|
2H, 14N
|
|
impair
|
impair
|
demi entier
|
1H, 13C, 19F,
|
Dans les calculs, il est parfois commode d'introduire le magnéton nucléaire :
En l'absence de champ magnétique, le moment magétique d'un noyau isolé peut prendre toutes les directions possibles et celles-ci correspondent à la même énergie (dégénérescence des niveaux d'énergie). Si l'on applique un champ magnétique extérieur B0, le noyau de moment magnétique m va interagir avec le champ. La résolution du problème en mécanique quantique conduit à une énergie d'interaction formellement identique à celle obtenue par un traitement classique :
Soit, compte tenu de la relation entre spin nucléaire et moment magnétique de spin.
(il peut y en avoir davantage pour d'autres noyaux.) A ces deux valeurs de mI correspondent deux valeurs possibles pour l'énergie en présence d'un champ magnétique. L'énergie d'interaction la plus basse vaut :
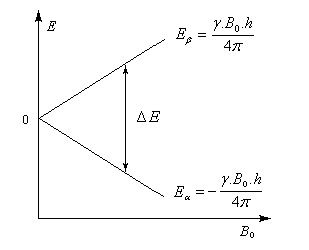
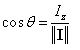
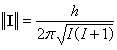
- pour mI = 1/2 ; q = 54,73° ;
- pour mI = -1/2 ; q = 180° - 54,73° ; q = 125,27° ;
Il s'agit d'un système assez simple car il ne possède que deux niveaux.
La fréquence n0 de la radiation électromagnétique permettant une absorption d'énergie entre les deux niveaux dont les énergies sont séparées de DE est telle que :
avec :
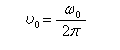
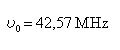
Transitions de résonance magnétique dans la matière
Population des niveaux d'énergie
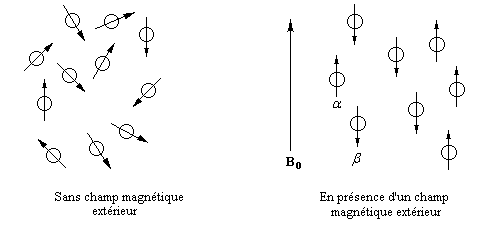
Dans un échantillon de matière, il y a un très grand nombre de noyaux. En présence d'un champ magnétique, les moments magnétiques vont s'orienter de façon parallèle (a) ou bien antiparallèle (b) au champ. Le schéma ci-dessous résume la situation en l'absence de champ magnétique (à gauche) et en présence d'un champ (à droite). La direction indiquée par les flèches est une direction moyenne puisque les moments magnétiques effectuent un mouvement de précession autour de l'axe Oz, direction du champ magnétique B0.
Description phénoménologique, vecteur aimantation
Au niveau macroscopique (ou plus précisément : mésoscopique), on introduit le vecteur aimantation M défini comme étant la somme vectorielle des moments magnétiques individuels, par unité de volume V (en anglais : magnetisation.)
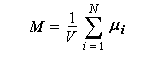
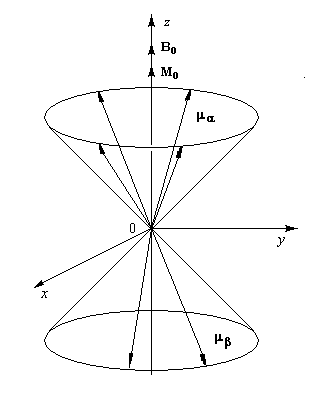 |
Lorsque l'échantillon est plongé dans un champ magnétique statique, les différents moments magnétiques effectuent un mouvement de précession autour du champ B0 à la vitesse angulaire de Larmor. Ils sont assujetis à se déplacer sur deux cônes de précession. Du fait du léger excès de la population des spins a par rapport aux spins b, l'aimantation totale d'équilibre, caractérisée par le vecteur M0, possède la même direction et le même sens que le champ magnétique B0 on dit qu'elle est longitudinale. L'aimantation M0 d'équilibre croit avec la densité de protons et avec l'intensité du champ magnétique statique. Les différents moments magnétiques sont répartis de façon équiprobables sur les deux cônes de précession. Il n'existe aucune relation de phase entre eux. Les composantes horizontales des moments magnétiques peuvent donc prendre toutes les orientations possibles dans l'espace. Il en résulte que l'aimantation transversale Mxy, dans le plan xOy est nulle. Notons que la mesure directe de l'aimantation d'équilibre M0 est quasi-impossible car sa valeur, très faible la rend très difficile à extraire du bruit de fond. |
De la même manière que pour un moment magnétique individuel étudié plus haut, l'idée est de provoquer une modification du vecteur aimantation au moyen d'un second champ magnétique de direction convenable appliqué pendant une durée limitée très courte. Il y a alors, comme on va le voir, création d'une aimantation dans le plan transversal.
En plus du champ statique B0, soumettons l'échantillon à un champ B1 tournant autour de Oz avec la vitesse angulaire de Larmor. Dans le repère tournant, ce champ garde une direction fixe. Dans le schéma ci-dessous, cette direction est OY.
Au niveau macroscopique, tout se passe comme si le vecteur aimantation était soumis à un couple de la part du champ B1. Ce couple va provoquer un basculement du vecteur aimantation dans un plan perpendiculaire à B1.
Le basculement se mesure par un angle f dans le plan XOZ.
La valeur de f est proportionnelle à l'intensité du champ magnétique et à la durée t d'excitation. En choisissant convenablement la durée de l'impulsion, on peut donc ajuster la valeur de f.
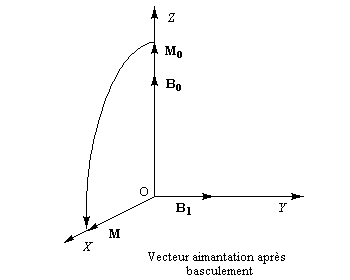
Une étude plus approfondie montre que si l'on se place cette fois à l'échelle microscopique, le basculement de f = 90° comme dans le dessin ci-dessus, entraîne deux phénomènes :
- un échange d'énergie qui conduit à une égalisation des populations des moments magnétiques (la somme vectorielle est alors égale à zéro) ;
- une mise en phase des moments magnétiques individuels.
On appelle relaxation nucléaire l'évolution d'un système de spins nucléaires vers l'équilibre thermodynamique. Désignons par N l'écart du nombre de noyaux par rapport à la répartition de Boltzmann, celui-ci va évoluer selon une cinétique du premier ordre.
Cet écart va donc suivre une loi exponentielle avec une constante de temps t.
- le système de spins ;
- l'environnement extérieur, appelé réseau.
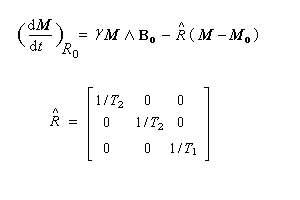
- au retour à l'équilibre de la composante longitudinale Mz correspond la relaxation longitudinale. Temps T1 (3ème ligne) ;
- au retour à zéro de la composante transversale Mxy correspond la relaxation transversale. Temps T2 (1ère ligne et 2nde ligne).
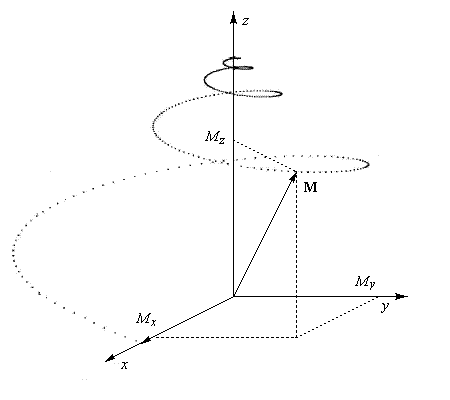
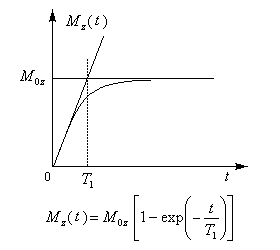 |
Le retour de la composante Mz de l'aimantation à sa valeur initiale M0z correspond à la relaxation longitudinale. Elle est due à un échange d'énergie entre les noyaux et leur environnement. Elle porte aussi le nom de relaxation spin-réseau. La constante de temps T1
est d'autant plus petite que les noyaux sont liés à des molécules de
plus grande masse molaire. Compte-tenu de la faiblesse des interactions
entre les spins et le réseau, elle est de l'ordre de quelques secondes
pour un liquide mais elle peut atteindre plusieurs heures dans le
cas des solides. Ce processus de relaxation est associé à un transfert
d'énergie. A l'échelle macroscopique il s'agit d'un transfert de chaleur (variation d'enthalpie.) |
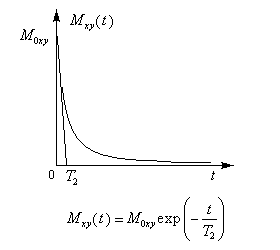 |
Après le basculement, la composante transversale de l'aimantation va diminuer puis s'annuler avec un temps de relaxation T2.
Ce phénomène est dû à l'interaction entre les spins nucléaires qui
provoque une perte de cohérence de phase des moments magnétiques dans
leur mouvement autour de B0. Cette désynchronisation des aimantations élémentaires est appelé relaxation spin-spin. Elle s'effectue plus rapidement que le retour à l'équilibre de la composante longitudinale. Le temps de relaxation T2 est donc toujours inférieur au temps de relaxation T1.
Ce processus de relaxation est associé à une perte de cohérence des moments magnétiques donc a une modification de l'ordre à énergie globale constante. Il a un aspect entropique. Cette perte de cohérence ne peut être justifiée que par un calcul quantique.
|
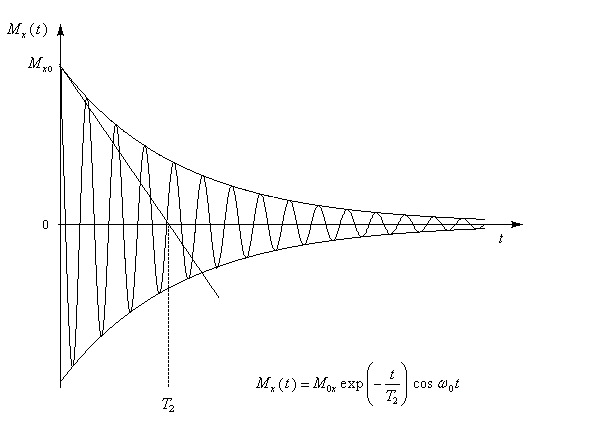
Remarque : la perte de cohérence de phase des moments magnétiques est un phénomène dont l'explication correcte ne peut être donnée qu'en utilisant la mécanique quantique : consulter [2]
Lorsqu'un couplage dipolaire entre spins est possible, il existe un autre type de processus de relaxation à l'origine de l’effet Overhauser nucléaire.
Constitution d'un spectromètre RMN
Appareils à onde continue
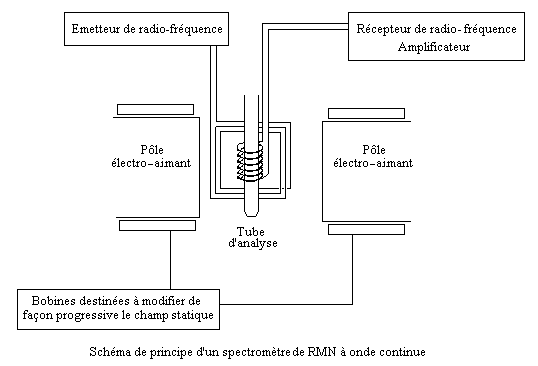
Pour observer la résonance d'un ensemble de spins, il y a a priori deux façons de procéder :
Le schéma ci-dessous décrit le principe d'un appareil appartenant à la première catégorie.
La technique de spectroscopie de RMN impulsionnelle (on dit aussi parfois RMN "pulsée" de l'anglais : pulse.) a été découverte par le physico-chimiste suisse Richard Ernst en 1966. Elle consiste à irradier l'échantillon étudié à l'aide d'une série d'impulsions électromagnétiques de durée très courte (quelques microsecondes) qui contiennent la gamme de fréquences à étudier [26]. Supposons que la substance ne comporte qu'un seul type de noyaux. Il y aura absorption d'énergie lorsque l'une des fréquence de la gamme de fréquences envoyée correspondra à la fréquence de résonance de ce noyau. Comme on l'a vu plus haut, une telle excitation fait basculer le vecteur aimantation d'un certain angle (par exemple 90°). Lorsque l'impulsion cesse, l'aimantation reprend après une certaine durée, sa valeur initiale de direction colinéaire au champ magnétique.
Lors du retour du vecteur aimantation à sa valeur initiale, la décroissance de la composante longitudinale induit une tension pseudo-périodique aux bornes d'une bobine de détection. Si cette bobine est placée le long de l'axe Ox, la grandeur détectée sera la composante de l'aimantation transversale suivant cet axe, c'est à dire Mx. Au cours du temps, cette tension varie dans le repère du laboratoire selon une loi sinusoïdale exponentiellement amortie.
S'il n'y a dans l'échantillon qu'un seul type de noyau, le signal est constitué d'une seule sinusoïde amortie. L'allure de la courbe donnant le signal en fonction du temps a alors l'allure suivante.

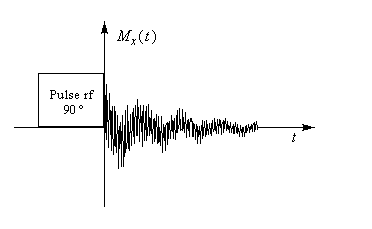
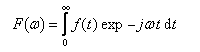
En résumé une expérience de spectroscopie comporte trois phases : impulsion, acquisition du signal, transformation de Fourier.
L'un des grands intérêts de la RMN impulsionnelle est qu'on peut se livrer à une suite d'expériences successives afin d'accumuler le maximum de données avant de procéder à la transformation de Fourier. Comme le bruit de fond est aléatoire cela a pour effet d'accroître considérablement le rapport signal sur bruit. Les appareils modernes fonctionnent sur ce principe (en anglais : FT-NMR : Fourier transform nuclear magnetic resonance.)
Les travaux de R. Ernst, et les développements qu'ils ont suscités lui ont valu le prix Nobel de Chimie en 1991. Pour la petite histoire, notons que l'article original dans lequel la spectroscopie de RMN impulsionnelle est introduite, a été refusé deux fois par le Journal of Chemical Physics avant d'être finalement publié.
Aspect technique
 |
Le premier spectromètre à impulsions et analyse par transformée de Fourier a été commercialisé par la firme Bruker en 1972. Un champ magnétique statique Bo aussi homogène et stable que possible est appliqué à l'échantillon. Ce champ (par exemple : 14.1 T, à 600 MHz) est obtenu grâce à une bobine supra-conductrice plongée dans un cryostat rempli d'hélium liquide. L'homogénéité du champ magnétique est obtenue grâce à des bobines appelées shims. Certaines de ces bobines se trouvent dans le cryoaimant (shims froids) tandis que d'autres sont à l'extérieur à la température ambiante (shims chauds). La stabilité du champ statique est assurée à l'aide d'une bobine auxiliaire par l'asservissement ("lock") du courant. |
 |
Le composé à étusier, préalablement mis en solution dans le deutérochloroforme CDCl3 est introduit à l'aide d'une pipette pasteur dans le tube d'analyse. Les avantages de CDCl3 sont nombreux :
|
D'après le principe d'incertitude de Heisenberg, la largeur de raie est proportionnelle à l'inverse de la durée de l'état excité. Plus cette durée est courte, plus la raie est large. En revanche, une raie fine correspond à un état excité de grande durée de vie.
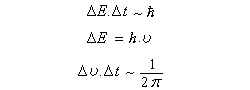
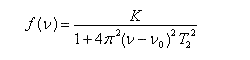
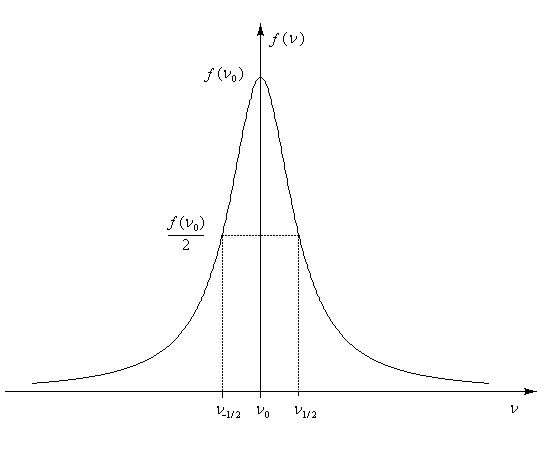
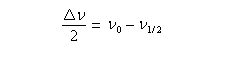
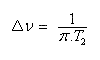
Déplacement chimique
Définition
La découverte du "déplacement chimique" (en anglais : chemical shift) date de 1950, indépendamment par W. G. Proctor, F. C. Yu (Stanford University), et W. C. Dickinson (MIT.)
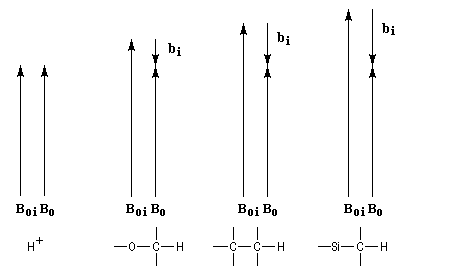
Il s'agit d'un effet très fin dont l'origine provient du fait que dans un échantillon de matière, tous les noyaux ne se trouvent pas dans le même environnement. Le champ appliqué engendre de la part des électrons entourant le noyau, un champ induit bi qui s'oppose au champ appliqué. A l'échelle macroscopique cela revient à dire que les électrons forment un écran autour du noyau . On dit aussi que le noyau est blindé. Cet effet de blindage (en anglais : shielding) peut être caractérisé par une grandeur si qui dépend de l'atome, appelée constante d'écran. Sa valeur est très faible (en moyenne de l'ordre de 10-5.)
En première approximation bi est proportionnel au champ appliqué.
- champ extérieur B0 fixe, on fait varier la fréquence (en anglais : frequency sweep method.)
La condition de résonance s'écrit :On en déduit la fréquence de résonance.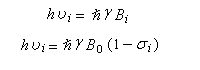
La fréquence de la radiation permettant d'atteindre la résonance est donc plus petite que pour un proton dépourvu d'environnement chimique.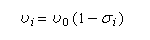
- n0 fixe, on fait varier le champ (en anglais : field sweep method.)
Soit B0i le champ extérieur nécessaire pour atteindre la résonance. La condition de résonance s'obtient au moyen de la relation entre la fréquence de la radiation électromagnétique incidente et la différence d'énergie entre les deux niveaux en présence du champ magnétique B0i.
Le champ magnétique utilisé pour atteindre la résonance est plus élevé que pour un proton dépourvu d'environnement chimique. Plus la densité électronique autour du noyau est grande, plus la constante d'écran est élevée et plus le champ B0i à appliquer est grand.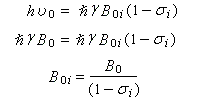
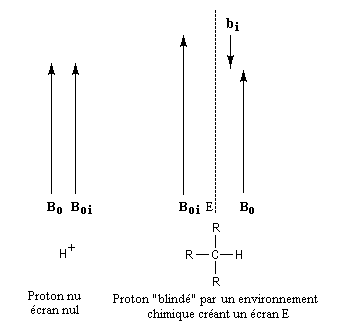
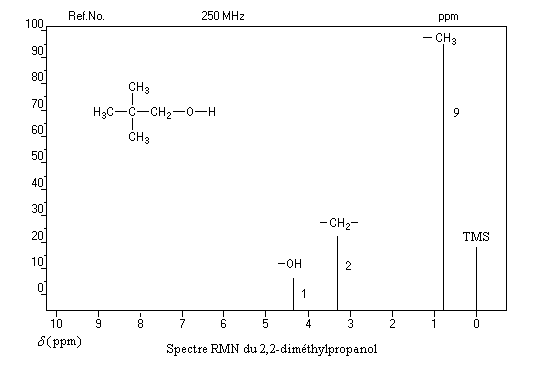
Face à l'impossibilité pratique de trouver des noyaux dépourvus d'environnement chimique, on utilise une substance de référence pour repérer les champs auxquels résonnent les différents types de protons. Le tétraméthylsilane (TMS) a été choisi car ce composé combine plusieurs avantages :
- tous les protons du TMS sont chimiquement équivalents ;
- ces protons sont fortement blindés car le silicium est moins électronégatif
que le carbone. Donc ils entrent en résonance pour des champs appliqués
élevés de sorte que pour la plupart des protons des autres composés
organiques :
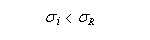
- le TMS est un composé très volatil (peu d'associations intermoléculaires) ce qui rend son élimination facile.
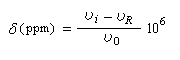
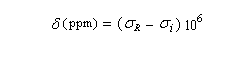

Plus la couverture électronique est grande, plus le blindage est élevé et inversement. Lorsque la couverture électronique augmente, le champ nécessaire pour produire la résonance croît ainsi que l'illustre le dessin ci-dessous.
Ainsi, le déplacement chimique va augmenter quand l'électronégativité du groupe lié au proton augmente. L'exemple ci-dessous concerne la famille des halogènes.
|
Composé
|
CH3I
|
CH3Br
|
CH3Cl
|
CH3F
|
|
Déplacement chimique d (ppm)
|
2,3
|
2,7
|
3,4
|
4,5
|
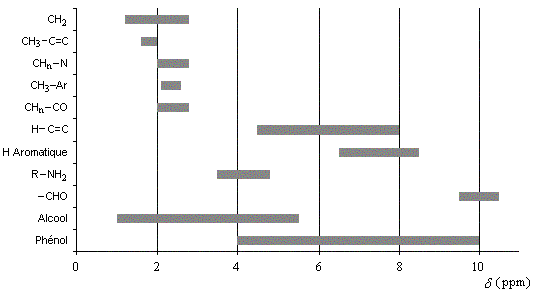
- le déblindage des protons liés à un cycle benzénique ;
- le déblindage très important des protons aldéhydiques.
- le blindage des protons des alcynes
La notion de prochiralité a été définie en stéréochimie. Des protons placés dans le même environnement chimique possèdent le même déplacement chimique. On dit qu'ils sont isochrones. On peut ainsi dresser le tableau suivant.
|
Composés
|
Identiques
|
Enantiomères
|
Diastéréoisomères
|
|
Type de proton
|
homotopiques
|
énantiotopiques
|
diastéréotopiques
|
|
Isochronie
|
toujours
|
non en solvant chiral
|
non
|
Un cas intéressant est celui de deux protons d'un groupe méthylène situé en a d'un centre chiral. Dans la molécule ci-dessous, les protons Ha et Hb sont diastéréotopiques. Quelle que soit la conformation, l'environnement chimique de Ha est différent de celui de Hb. Leur déplacement chimique est donc différent.
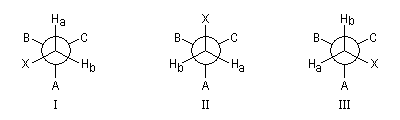
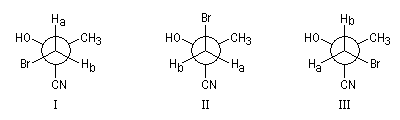
Définition
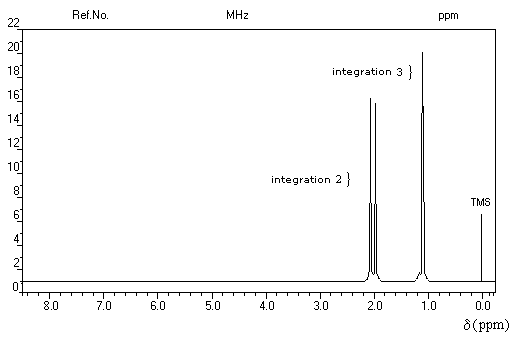
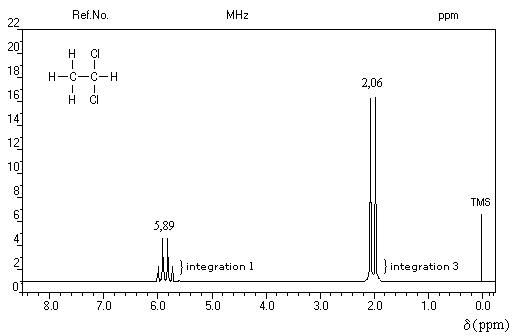
Un dispositif appelé intégrateur permet de mesurer la surface des différents pics ou d'ensembles de pics proches (appelés massifs). Cette surface est proportionnelle au nombre de protons correspondants. L'appareil trace alors sur le spectre une courbe possédant des marches appelée courbe d'intégration. Le rapport des hauteurs entre deux paliers est égal au rapport des nombre de protons impliqués dans les massifs correspondants. La courbe ne donne donc pas le nombre absolu de protons d'un massif mais leur proportion relative dans ce massif.
Utilisation
La connaissance de la courbe d'intégration permet de préciser la structure de la molécule comme le montrent les exemples ci-dessous.
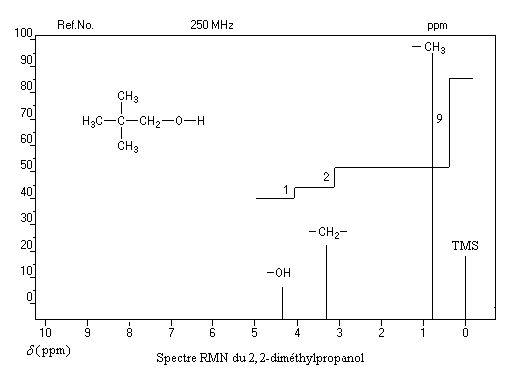
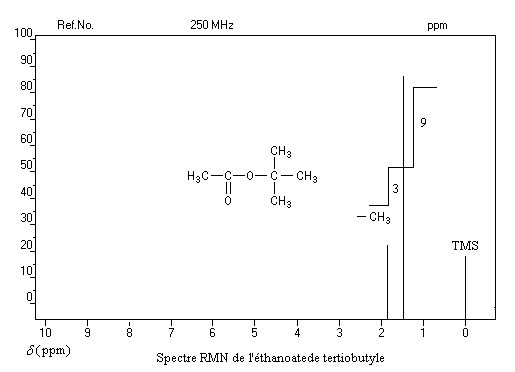
Origine du couplage scalaire spin-spin
Lorsque les spectres RMN sont observés avec une résolution suffisante, on observe que certains signaux sont constitués de plusieurs pics. Ce phénomène est dû aux interactions entre les noyaux soit dans l'espace, soit par le biais des électrons de liaison. On donne le nom de couplage à ce type d'interaction.
Il existe plusieurs types de couplages [40]. Nous commencerons par évoquer le couplage scalaire. Le terme scalaire vient du fait que ce type de couplage ne fait pas intervenir la direction. On appelle système de spins un ensemble de spins couplés de façons scalaire. On distingue les couplages :
-
hétéronucléaires : le système de spins est constitué de noyaux de nature différente (par exemple 1H et 13C). Il s'agit de couplage 1J ;
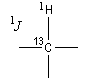
- homonucléaires : le système de spins est constitué de noyaux de même nature (par exemple des protons) il s'agit de couplages nJ avec n > 1.
|
Couplage
|
Nombre de liaisons
|
Nom
|
|
2J
|
2
|
géminal
|
|
3J
|
3
|
vicinal
|
|
4J
|
4
|
longue distance
|
Interaction entre deux protons
L'interaction entre deux protons notés A et X peut être décrite en terme de champ. Raisonnons sur la résonance du proton A. Selon l'orientation de son moment magnétique le proton X va créer un petit champ qui va s'ajouter (1) ou se retrancher (3) au champ appliqué :
- le champ créé
par X s'ajoute au champ appliqué. Par rapport à la situation (2) d'un
proton isolé, le champ nécessaire pour atteindre la résonance a diminué (1) ;
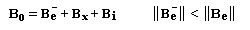
- le champ créé par
X se retranche du champ appliqué. Par rapport à la situation (2) d'un
proton isolé, le champ nécessaire pour atteindre la résonance a augmenté (3) ;
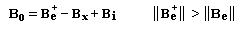
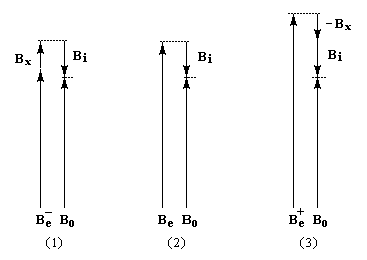
Dans le spectre, le signal de A va être éclaté en deux pics. L'écart entre les pics est égal à la constante de couplage exprimée en Hz.
Heureusement, tous les couplages entre noyaux ne sont pas observables (même si le couplage existe) car cela entraînerait une très grande complication des spectres. Pour que les couplages entre noyaux n'apparaissent pas dans un spectre, ceux-ci doivent être magnétiquement équivalents.
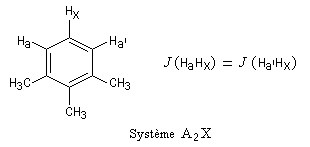
Considérons un ensemble de noyaux Ai. On dit que ces noyaux sont magnétiquement équivalents si, et seulement si :
- ils sont chimiquement équivalents, c'est à dire qu'ils possèdent le même déplacement chimique ; on dit que ce sont des noyaux isochrones ;
- ils sont couplés de façon identique (même constante de couplage) avec tous les noyaux extérieurs à cet ensemble ; on dit que ces noyaux sont isogames.
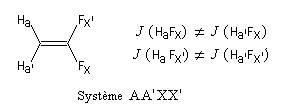
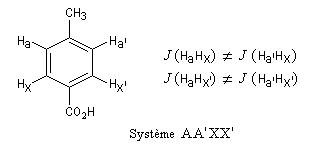
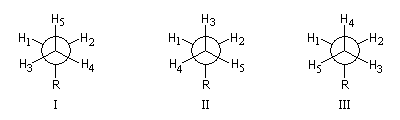
- basse température : pas de rotation libre (structure "figée" I)
ProtonsH1H2H3H4H5SystèmeAA'BB'C
- température plus élevée : rotation libre (conformations I, II, III, etc.)
ProtonsH1H2H3H4 H5SystèmeA2B3
Ordre des couplages
Le couplage est faible, lorsque :
On dit que le spectre est analysable au premier ordre. En pratique, on utilise le critère :
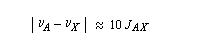
De même, la mesure directe de J n'est plus possible.
On peut revenir à un spectre du premier ordre en augmentant le champ magnétique. En effet, la constante de couplage est indépendante du champ appliqué mais la différence de fréquence entre deux noyaux croit avec lui.
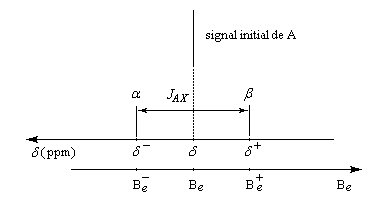
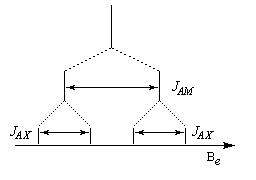
- Système AMX
Le signal initial de A est d'abord dédoublé par son interaction avec M. Ces signaux sont à leur tour dédoublés par l'interaction avec X. On obtient un doublet de doublet.
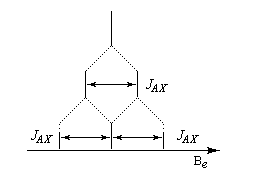
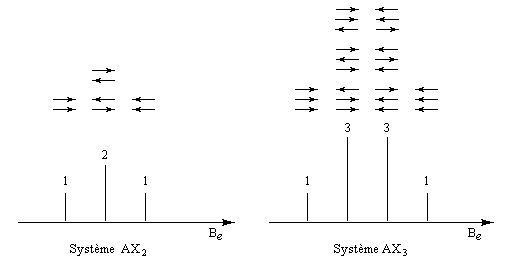
- Système AX2
Il s'agit d'un cas particulier de système AMX avec 3JAM = 3JAX. La raie centrale a donc une hauteur double des deux autres.
- On a de même des systèmes AX3 et plus généralement AXn.
Les hauteurs relatives des pics des multiplets sont données par le triangle de Pascal.

On appelle couplage géminal, le couplage entre deux protons liés à un même atome de carbone. Ce type de couplage n'est pas fréquemment observé car les protons géminés sont souvent rendus magnétiquement équivalents en moyenne par les mouvements conformationnels. La constante de couplage est négative. Sa valeur absolue dépend fortement de l'angle entre les liaisons.
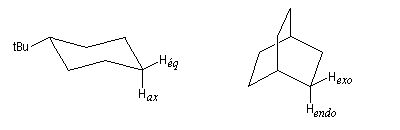
En série acyclique, on observe ce type de couplage entre protons diastéréotopiques. Un cas particulièrement important est celui d'un groupe méthylène adjacent à un centre chiral.
Couplage vicinal
Il s'agit du couplage entre des protons séparés par trois liaisons. La constante de couplage est souvent notée 3J.
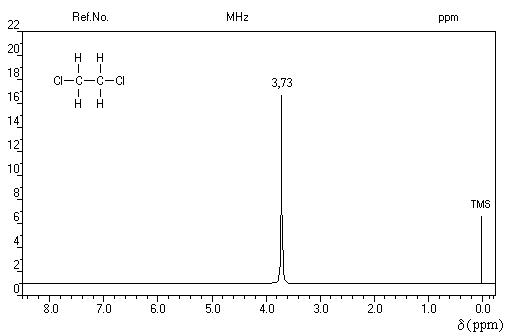
Dans la molécule suivante, le couplage n'apparaît pas car les protons sont magnétiquement équivalents.
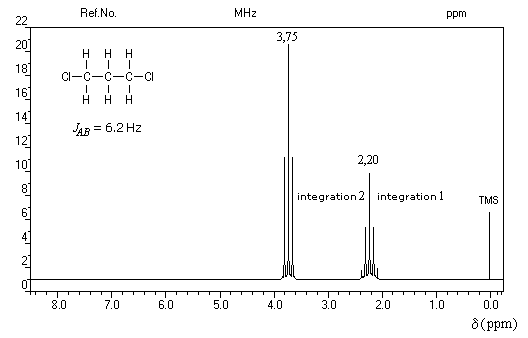
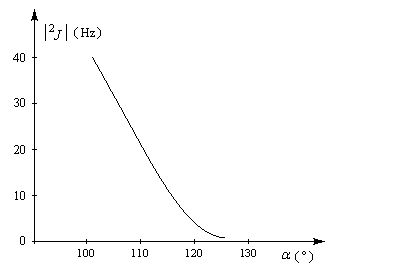
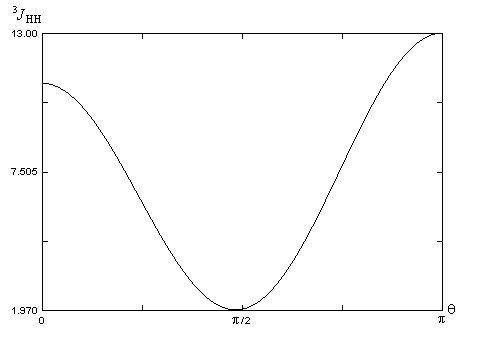
La constante de couplage 3JHH entre deux protons vicinaux dépend de la valeur de l'angle dièdre entre les liaisons C-H. Cette dépendance peut être exprimée quantitativement grâce à la formule de Karplus.
|
Coefficient
|
A
|
B
|
C
|
|
Valeur (Hz)
|
7,0
|
-1,0
|
5,0
|
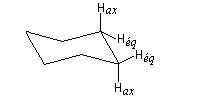
|
Protons
|
HaxHax
|
HaxHéq
|
HéqHéq
|
|
q (°)
|
180
|
60
|
60
|
|
3J
|
11,8
|
3,9
|
3,9
|
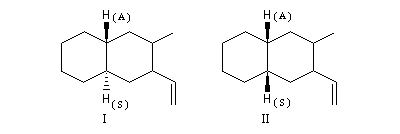
Comme application, considérons les spectres RMN des composés I et II. Le basculement conformationnel est bloqué grâce à la présence du groupe tertiobutyle :
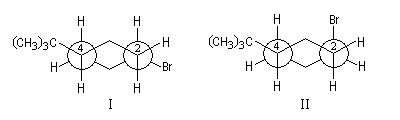
- dans le spectre de I, l'atome d'hydrogène porté par le carbone 1 est en position axiale. Il est couplé à deux atomes d'hydrogène vicinaux axiaux (Jaa = 10 Hz) et deux atomes d'hydrogène vicinaux équatoriaux (Jae = 5,5 Hz), le signal se présente donc comme un triplet de triplets ;
- dans le spectre de II, l'atome d'hydrogène porté par l'atome de carbone 1 est en position équatoriale. Il est couplé à deux atomes d'hydrogène vicinaux équatoriaux et deux atomes d'hydrogène vicinaux axiaux. Mais les constantes de couplage Jae et Jee sont assez proches et le signal va se présenter pratiquement comme un quintuplet.
Couplage à longue distance
Lorsque le nombre de liaisons séparant les protons couplés est supérieur ou égal à 4, on parle de couplage à longue distance. Ce type de couplage est observé dans des structures en M ou en W telles que celles qui sont représentées ci-dessous.
On observe des couplages à très longue distance (jusqu'à 9J) chez les polyynes.
Couplage fort
Des pics parfaitement symétriques n'apparaissent que dans le cas où la différence des fréquences de résonance nA - nX des groupes de noyaux A et X est beaucoup plus élevée que la constante de couplage J. On peut montrer par un calcul de mécanique quantique, que les niveaux énergétiques des deux noyaux ne peuvent jamais s'intercaler. Afin d'éviter un tel croisement des niveaux, les pics intérieurs ont une intensité qui croit aux dépens des pics extérieurs dont l'intensité diminue. Les barycentres des doublets restent fixes à la valeur (nA + nX)/2.
On donne le nom de quadruplet AB à ce type de spectre. Le rapprochement des lettres A et B dans l’alphabet indique que la différence nA- nB n’est pas grande devant la constante de couplage.
La figure ci-dessous montre l'évolution d'un système AX au fur et à mesure que le rapport Dn/J, diminue. Lorsque la différence des déplacements chimiques augmente, le système AB se rapproche graduellement d'un système AX. Au contraire quand elle tend vers zéro, les pics externes disparaissent quelle que soit la valeur de J. On obtient un pic unique. C'est pour cette raison que des protons magnétiquement équivalents apparaissent sous la forme d’un signal unique.
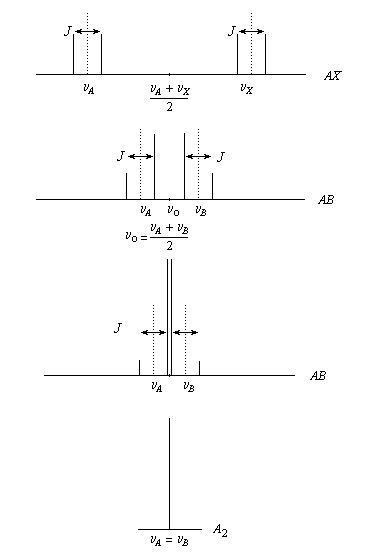
- chez les composés éthyléniques ;
- chez les composés aromatiques
Le phénomène d'échange de protons est un cas particulier d'échange chimique qui s'observe chaque fois qu'un proton est suffisamment mobile pour pouvoir être échangé entre deux molécules. On va rencontrer ce phénomène dans les familles de composés où le proton est lié à un hétéroatome : les alcools, les amines, les acides carboxyliques.
Comme on peut le prévoir, compte-tenu du mécanisme, la vitesse du phénomène d'échange dépend de la température. Les figures ci-dessous représentent les spectres RMN du méthanol pur enregistrés respectivement à -65 °C et à 40 °C.
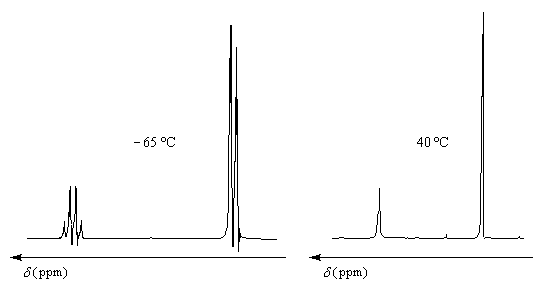
Pour une analyse théorique de l'échange chimique : consulter [50]
Découplage de spin
Il est possible de préciser la nature des protons couplés en procédant à une expérience de découplage de spins. Dans le découplage homonucléaire sélectif, on irradie un groupe de protons avec un champ correspondant à leur fréquence de résonance. Ils absorbent alors de l'énergie et leur influence sur les protons qui étaient initialement couplés avec eux est supprimée. Dans l'exemple suivant, l'irradiation des protons H-2 supprime le couplage avec les protons H-3 dont le signal apparaît comme un singulet. On a représenté ci-dessous le spectre original de la molécule d'acide (E) cinnamique et le spectre après découplage.
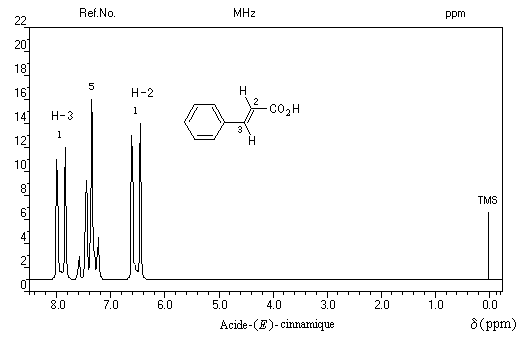

Considérons deux spins A et S suffisamment proches dans l'espace pour qu'une interaction dipolaire entre-eux puisse se manifester. Cette distance doit être typiquement inférieure à 500 pm car l'interaction, qui varie en 1/r6, s'amortit rapidement avec l'éloignement. L'interaction dipolaire ne se traduit pas par un éclatement des raies d'absorption en milieu isotrope (comme c'est le cas avec le couplage scalaire) car la valeur moyenne de l'énergie d'interaction, qui dépend de la direction des spins, est globalement nulle.
En revanche, soumettons le spin A à une irradiation à sa fréquence de résonance jusqu'à ce qu'il y ait saturation. Cela a pour effet de faire disparaître le signal relatif à A. Mais, si les spins A et S sont couplés, un phénomène de relaxation croisée va pouvoir transférer de l'aimantation, du spin saturé A au spin S couplé avec lui. C'est l'effet Overhauser nucléaire (en anglais : nuclear Overhauser effect ou nOe) découvert en 1950 par le physicien américain Albert Overhauser. Pour davantage d'informations, consulter [45].
L'effet Overhauser nucléaire est très sensible à la distance entre les protons couplés. C'est pourquoi il est à la base de méthodes très utiles pour la détermination de structures en RMN. En particulier il est utilisé pour différencier des diastéréo-isomères. Dans l'exemple suivant, les protons (A) et (S) manifestent un effet nOe beaucoup plus important dans la molécule II que dans la molécule I du fait de leur plus grande proximité dans l'espace dans le second cas.
Ouvrages théoriques
[1] Spectroscopies de la Molécule, J. Barriol et J. -L. Rivail, Presses Universitaires de France.
[2] P. J. Hore - Nuclear Magnetic Resonance, Oxf Chemistry Primers, Oxford University Press (1995).
[3] R. J. Abraham, J. Fischer, P. Lofthus - Introduction to NMR Spectroscopy, Wiley New-York (1991).
[4] R. K. Harris - Nuclear Magnetic Resonance Spectroscopy, Longman, London (1986) .
[5] P. Atkins - Molecular Quantum Mechanics, Oxford University Press (1983) .
[6] P. Laszlo P. J. Stang - Spectroscopie Organique, Hermann (1972).
[7] V. Minkine - Théorie de la structure moléculaire, Editions Mir (1979).
[8] T.C. Farrar An Introduction To Pulse NMR Spectroscopy Farragut Press, Chicago, 1987.
[9] H. Günther, La spectroscopie de RMN, Masson, Paris, 1993.
[10] F.A. Bovey & L.W. Jelinski, Nuclear Magnetic Resonance, in Encyclopedia of Polymer Science and Engeneering, Vol. 10, p. 245, Wiley, N.Y., 1986.
.
Liens
[20] Cours de RMN ; Université en ligne.
Excellent cours de RMN en français !
[21] The Basics of NMR by J.P. Hornak
Sans doute l'un des meilleurs cours de RMN sur le web.
[22] Imagerie par résonance magnétique nucléaire
Principes de la RMN, obtention des images, interprétation du contraste etc.
[23] MRI Resource Directory NMR
Site portail relatif à la RMN
[24] La RMN en phase liquide par D. Canet, Laboratoire de Méthodologie RMN Université de Nancy.
[25] Research in Nuclear Magnetism Edward M. Purcell, The Nobel Prize in Chemistry 1952
[26] Nuclear Magnetic Resonance Fourier Transform Spectroscopy Richard R. Ernst, The Nobel Prize in Chemistry 1991
[27] NMR Studies of Structure ans Function of Biological Macromolecules Kurt Wüthrich, The Nobel Prize in Chemistry 2002
[28] Histoire de la RMN autour de ses premiers acteurs par Maurice Goldman
[29] Aide et outils en RMN
[30] Principes physiques de la RMN
[31] Cours de RMN
[32] Exemples de spectres de RMN Dr. Scott Van Bramer Widener Univeristy
[33] Cours de RMN à l'ESPCI
[34] Cours de RMN, Université de Montréal
[35] Etude de chaîne glycannique par RMN
[36] NMR by Suzanna Strauss University of British Columbia.
[37] Principes élémentaires de la RMN
[38] Centre RMN à très haut champ, Lyon
[39] Cours de RMN par M. Petit
[40] Nuclear Spin Hamiltonian : Couplings by J. Titamn, University of Nottingham
[41] The principle of nuclear induction F. Bloch, The Nobel Prize in Chemistry 1952
[42] Notion de RMN par impulsions. Cours de l'ESPCI
[43] RMN et IRM à l'institut matière et rayonnement de Saclay
[44] The Nobel Prize in Physiology or Medicine 2003 Paul C. Lauterbur, Sir Peter Mansfield
[45] Effet Overhauser Nucléaire
[46] Cours de RMN, CNAM.
[47] Blindage, déblindage.
[48] Cours de RMN, Ecole Polytechnique.
[49] Principe de la création d'un champ tournant.
[50] Echange en RMN P. Vasos, Ecole Polytechnique Fédérale de Lausanne.
[51] The Nobel Prize in Physics 1944, Isidor Isaac Rabi
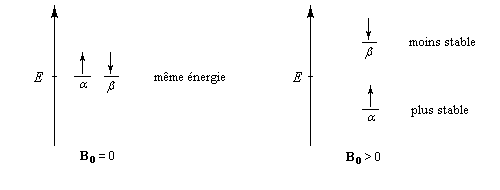
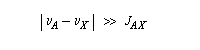
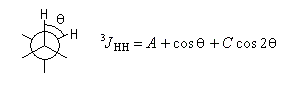
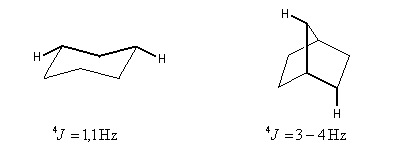
Aucun commentaire:
Enregistrer un commentaire